
 |
 |
| 图1割圆图 |
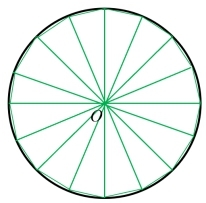 |
| 图2割圆图 |
 |
| 图3割圆图展开图 |
 |
刘徽(约225-295)出生于人杰地灵的齐鲁大地,成长于英才辈出的魏晋时期。他的著作《九章算术注》和《海岛算经》是中国最宝贵的数学遗产,也是世界数学的瑰宝。中科院院士、数学机械化专家吴文俊说:“从对数学贡献的角度来衡量,刘徽应该与欧几里得、阿基米德等相提并论。”
《九章算术》收集了战国、秦、汉时期的数学成果,共246个问题,分为九章。其数学成就主要是分数四则运算、比例运算、各种面积和体积的计算方法,以及勾股定理的应用等。《九章算术》构筑了中国传统数学的基本框架。
刘徽年幼时学习了《九章算术》,随着年龄的增加,对《九章算术》有了新的认识。他“观阴阳之割裂,总算数之根源,探赜之暇,遂悟其意”。他对书中的错误、晦涩难懂的地方进行校正,对来历不明的结论、公式等补充严格的证明,还对部分概念进行了辨析,确立了严格的定义。经过数十年的辛勤考证,终于完成了《九章算术注》。
《九章算术注》赋予了《九章算术》新的生命,使中国传统数学形成了严密的数学理论体系。
在《九章算术》的方田章中,有多个与圆有关的面积问题。
问题三十一:今有圆田,周三十步,径十步。问为田几何?
答曰:150平方步。
术曰:半周半径相乘得积步。
刘徽想,周长30步,直径为10步,这个几何图形不是圆,而是一个圆内接正六边形,如图1所示。刘徽想用圆内接正十二边形代替圆,这种近似程度不是更好些吗?刘徽通过仔细地思索、论证,终于概括出“割之弥细,所失弥少。割之又割,以至于不可割,则与圆周合体而无所失矣”的“割圆术”精髓。
刘徽把他的1800字的割圆术,附在《九章算术》方田章的后面,从此有了刘徽的“割圆术”。在“割圆术”中,刘徽完成了两大创举。第一,他证明了圆的面积公式;第二,他计算出圆周率的近似值为3.14。
刘徽首先把圆周六等分,依次连结相邻的两点,等到一个圆内接正六边形。他继续倍增边数,得到圆内接正12边、24边直到无穷多边。这样就可以得到圆面积的精确值。刘徽设计了圆面积的算法。他从正六边形开始,迭代5次就得到正192边形的面积,把圆周率精确到小数点后两位,等于3.14,这在2000年前是一项了不起的工作。这个值也被后人称为“徽率”。
刘徽在“割圆术”中写的,“以一面乘半径,觚而裁之,每辄自倍。故以半周乘半径而为圆幂。”这就是他证明圆面积公式的方法。他将图2所示与圆合体的正无穷多边形裁剪成无穷多个顶点是圆心O,底边是正多边形的边的小等腰三角形。刘徽将无穷多个等腰三角形的底边连接在一起,如图3所示。无穷多个小三角形其底边之和就是圆的周长,因此得到圆面积公式。
圆的面积等于圆的半径乘以圆的周长的一半。
刘徽在给《九章算术》作注时,撰写了《重差》一卷,这是关于测量海岛的高和水平距离问题,编写了九个复杂的、有代表性的测量问题。到了唐代,数学家们将《重差》更名为《海岛算经》。在书中刘徽利用“重差术”,即两次求差的运算,科学地计算出泰山主峰的高度为1792.14米。这在中国历史上是首创。
刘徽一生不追求功名、严谨治学,敢于摈弃前人不合理、不科学的知识,勇于创新,他给我们中华民族留下了宝贵的财富。刘徽的工作,不仅对中国古代数学发展产生了深远影响,而且在世界数学史上也确立了崇高的历史地位。
(作者单位为华中农业大学理学院)






