
 |
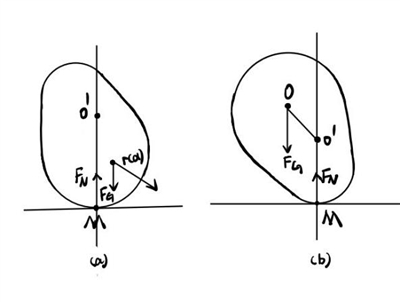
| 图1:不倒翁二维化示意图 |
 |
| 图2:印度星龟 图片来自wikimedia.commons |
 |
 |
□ 王 驰
说到翻转这个问题,我们最容易想到的是不倒翁,好像无论把它怎么推,使它如何歪斜,它都能回到最初直立的状态。要分析这个问题,我们可以把不倒翁二维化以后放在纸上(如图1),用物理和数学的公式进行推理。因为如果物体要平衡的话,经过与地面的接触点M的垂线一定会过物体平稳放置时的重心O,如果我们人为晃动物体使它与地面成一定的角度,由于接触点处的曲率中心O’高于重心O,那么重力FG和地面约束力FN的合力将把物体拉回它原来的状态,我们称这种平衡为稳定平衡。但是,如果倾斜时接触点曲率中心O’低于重心O,那么合力就会使物体继续朝向倾斜方向倾斜,我们称这种平衡为不稳定平衡。
那么,一个物体上到底有多少个平衡接触点呢?研究发现,平衡点包括了尖端、棱中、鞍点等,计算方式来自Poincar’e-Hopf定理:假设几何体存在i个稳定和j个不稳定点和k个鞍点,那么凸几何体的各种平衡点数目将遵循i+j-k=2的规律。
也就是说,物体总是会回到一个平衡点所在的位置,那在三维空间中,物体最多或者是最少有多少个平衡点呢?1995年数学家弗拉基米尔·阿诺德(Vladimir Igorevich Arnold)提出所有现存的三维实体的平衡点(包括平衡点和不平衡点)至少有四个。
但有一位匈牙利数学家加博尔·多莫科斯(Gabor Domokos),认为少于四个平衡点的物体是实际存在的,在很长时间的计算无果后,他甚至和妻子在海边拾取鹅卵石,不停地将它们滚来滚去,来观察他们有多少个稳定和不稳定点,试图找到一个平衡点少于4的鹅卵石,但始终找不到。不过最终经过了数十年坚持不懈的研究计算,他和他的伙伴科尔瓦尼最终通过数学方式证明了这种形状是存在的,并且这种物体只有两个平衡点,一个稳定平衡点和一个不稳定平衡点,他给这个物体命名为冈布茨。
冈布茨是一个质量均匀分布的三维凸几何体,有区别与不倒翁这种不均匀的材质——我们可以轻易利用不同物体密度重量的不同,来组成一个两平衡点物体(就像往不倒翁里放沙子一样)。找冈布茨体的难度就类似于找一个质量均匀的不倒翁。
那自然界里到底有没有类似冈布茨体的生物或者是物质呢?就像花瓣里藏着斐波那契数列一样,大自然一直都是一个伟大的数学家,只不过我们熟视无睹罢了。多莫科斯对此观点也是深信不疑。他和科尔瓦尼几乎跑遍了布达佩斯的所有的动物园,最终让他们发现了一种乌龟——印度星龟(如图2)。这也是标题中问题的答案:在大部分乌龟通过晃动四肢和头的帮助把自己翻回去的情况下,这种乌龟进化出了与冈布茨体相似形状的龟壳,不需要头和四肢的帮助就能快速回到四肢落地的正常位置,虽然这种乌龟的质量不是完全均匀分布的,但是也证实了自然界中确实有唯一稳定平衡和唯一不稳定平衡的生物体存在。目前已经发现了三种这样的乌龟,它们只要缩紧身体就能达到自动翻转的效果。
人生也是一样,我们要努力地打磨自己身上的“平衡接触点”,在遇到磨难艰辛的时候,找到自己的“平衡点”,翻回去。历尽千帆,归来依是少年。
(作者系华中农业大学名师工作室数学文化团队成员)






