
 |
 |
 |
 |
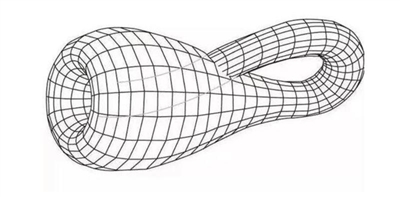
| 图1:莫比乌斯环。图2:电影中的莫比乌斯环建模。 图3:假想中的克莱因瓶。 图4:时空穿梭。 |
 |
《复仇者联盟4》电影中,钢铁侠将莫比乌斯环翻转,首尾连接,从而设计出了时光机器。主角穿梭时空,其数学模型竟是一条扭曲的环,让我们来探索这“怪圈”背后究竟有何魅力。
当我们谈及莫比乌斯环时,会惊叹其简单的构造,不论是数学还是物理,对它都有着各方面的猜想和研究。其制作方法也十分简单——当我们取一条宽条纸,将一端捏住不动,而另一端旋转180度,再将两端粘起来,就会得到一个莫比乌斯环。我们会发现,莫比乌斯环只有一个面和一条边,当我们沿着莫比乌斯环的中线剪开后,得到的不是两个环,而是一个更大的环,从理论上说,这种延展性是无限的,所以有些人也将莫比乌斯环看作是无限之路,甚至将它视作为无穷大∞的一种代表。
如果我们将剪开的莫比乌斯环看作撕裂开的时空,那么大小环是分别独立存在的,只有一个地方相连,而这个地方我们将其称为奇点,而撕裂空间则可以创造独立空间,即平行世界。因此,关于时空穿梭的想法,也似乎并不是不可能。因为两个时空,它们大部分时间是不相交的,只是平行存在于我们的世界,而相交处,则可以成为时空穿梭的契机。
让我们回到影片,其中提到量子领域的时间机制是不一样的。如果我们能操控这种机制,从而能够控制混乱的时空,那么,在某个特定的时间点,进入量子领域,然后再在另一个时间点从量子领域出来,通过量子波动打破普朗克尺度,然后触发德式效应,就能做到时空穿梭。确实,如果时间类似于一条莫比乌斯带的话,我们确实可以做到时空穿梭,而且穿越虫洞的想法也并非空中楼阁了。
在维度研究上面,《复仇者联盟4》中时光机器的雏形也引起了我自己的思考,有些人认为时间是有长度的,同时也有些人认为它是没有长度的。如果说时间是静止的,或者弯曲的,就像莫比乌斯环,由于我们这个世界的科技无法做到完成一个完整的循环,所以才认为它是无限的。根据中学的知识,两条平行线是不可能相交的,因为根据几何上的定义,在同一平面内,两条永不相交的直线称为平行线。也许这个在二维平面上是正确的,但是在三维空间里却不一定。假使我们在莫比乌斯环的中间画一条线,首尾相连,如果按照纸张的厚度算两条平行线的距离,纸的“正反”面的线看成两条平行线,我们就可以知道其实平行线也是可以相交的,但是前提就是要扭曲,进行空间扭曲。
数学领域有一个重要的学科称为拓扑学,主要研究几何图形或空间在连续改变形状后还能保持不变的一些性质,而莫比乌斯带是其中有趣的代表,与此相关的还有克莱因瓶。在拓扑学中,人们往往对图形的位置进行研究,而不关注图形本身长度和角度等性质。1882年,德国数学家克莱因提出克莱因瓶的猜想,他认为这种瓶子根本没有内、外之分,无论从什么地方穿透曲面,到达之处依然在瓶的外面,所以,其本质上是“有外无内”的。观察这张图片,有一点可能令人困惑,那就是克莱因瓶的瓶颈和瓶身是相交的,虽然三维空间上相交,但在四维空间上,却可以不相交,就像我们拿出两支笔放在空间中,一上一下地交叉放置,实际上并未相交,但从上向下看就是相交的。因此,它在三维空间并不存在的,而是四维空间的产物。
“怪圈”莫比乌斯环简单的构造,却又能给我们带来极度深刻的思考,这样一个超越常识的存在,在我们不断思考的过程中,确实会源源不断地给我们惊奇的发现。数学中这样的例子不在少数,简约却不简单。当我们扭转一根纸条,然后两头粘接起来,就可以制成一个莫比乌斯环,而环面是一种单侧、不可定向的曲面,当我们沿着纸带的中央行走,却能够在不知不觉中回到原点,我们可以说它和直线一样,是无始且无终的,这样一个简单的模型将扭曲的数学美体现得恰到好处。虽然是电影,谁也不能证实究竟有没有四维莫比乌斯环的存在,特殊的莫比乌斯环能否回到最初的时间节点,四维莫比乌斯环究竟能不能用于时光机器的发明,未来还有很多领域值得我们去发现和研究。数学同其他领域一样,具有很大的发展前景,只要刻苦钻研,潜心研究,总是会有一番收获。
(作者单位:华中农业大学理学院)






