□ 陈思进

    超越时空

    在《费曼：令人们“痴迷”的量子力学物理大师》（《科普时报》2018年10月12日 3版）一文中，我以费曼的“聪明的救生员”选择最短的路径救人为例，解释了“路径之和” 理论。

    文章发表后，有读者留言问我，救生员是受过训练的专业人员，当然能够“聪明”并“主动”地采用耗时最短的路径去救人，要是动物如宠物狗，遇到类似的情况，是否也会这样呢？

    答案是肯定的！

    美国数学教授蒂姆·彭宁斯（Tim Pennings）养了一条名为埃尔菲斯（Elvis）的威尔士柯基犬。蒂姆总是与埃尔菲斯在密歇根湖的岸边玩耍抛接球，他会将埃尔菲斯最喜欢的网球扔进水中，埃尔菲斯会立即冲出去，在海滩上跑，在湖水里游泳，每次都把网球捡回来。

    在抛球捡球的游戏中，蒂姆发现埃尔菲斯的行为非常有趣。当他把网球扔入湖水中，埃尔菲斯并不选择一条看似直接的路程，跳入湖中，游完全程，而是先在海滩边跑完一段路程，然后到达某一个点，才跳进水中游一段再用嘴把网球衔回来。蒂姆的脑海中闪现了一个问题：埃尔菲斯是通过一条耗时最短的路程取回网球的吗？

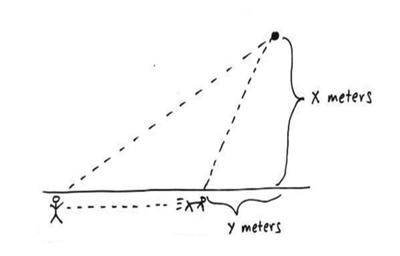
    于是，蒂姆划分并测量了埃尔菲斯在岸上跑动的路径，以及网球运动的距离。在收集了35个数据后（上图中的x和y数值，以米为单位），作为一个数学教授，他很快用微积分解决了问题的最优解，结果“恰好”和费曼的“聪明的救生员”一样：小狗埃尔菲斯也能够“聪明”并“主动”地采用耗时最短的路程，用嘴把网球捡回来。

    埃尔菲斯的举动令蒂姆非常震惊，他随即写下了《狗懂得微积分吗？》。在这篇论文中，蒂姆写道：“埃尔菲斯显然不懂微积分，但它的行为反应了大自然的神奇之处，即自然总会选择最优解。”

    不过，请别忘了，数学模型必须事先做出许多假设，使问题简单化且便于分析。例如：湖水没有波浪，水是静止的；埃尔菲斯匀速前进，不会因为疲倦而放慢速度；湖畔可以看作一条直线等等。因此，埃尔菲斯实际上所用去的时间，说不定比数学模型所计算的结果还要短。

    写到这儿，不禁想起小时候因为调皮，经常和几个发小在弄堂里，用热水驱赶小蚂蚁。那时我注意到一个奇怪的现象：一群蚂蚁在搬运食物进入它们的窝，并不是沿着最短的直线路径前行的。

    事实上，科学家的研究证实了，蚂蚁和“聪明的”救生员和小狗埃尔菲斯一样，都是走耗时最短的路径。科学家用一块玻璃表面，以及相对粗糙的绿色桌面来模拟沙滩和海水。他们发现蚂蚁的选择更加接近于最快，而非最短的直线路径。正如光的轨迹那样，蚂蚁也会选择减小时间而非距离（见附图：蚂蚁折射定理），来搬动食物进入它们的老窝。

    再谈回到费曼，正是经由上述的“路径之和”，他“无意”中发现了最简单的，也是最深刻的综合量子理论复杂性的方法，赢得了1965年的诺贝尔物理学奖。

    比如，你想走过一个房间，根据牛顿的经典力学，你会选择从A到B的最短距离，叫做经典路径。但是根据费曼的科学理论，你必须首先考虑连接A和B的所有可能的路径。这意味着要考虑到火星、木星、最近的星星的路径，甚至在时间上返回到大爆炸的路径。不管这些路径是多么愚蠢、多么奇怪，但你必须考虑它们。费曼给每条路径一个数值，给出一套精确的规则计算这个数值。

    对此，距离爱因斯坦探寻了下半辈子的TOE（Theory of everything，万有理论）最接近的超弦理论创始人之一、我的母校美国纽约市立大学物理学教授加来道雄曾谈及：

    费曼发现了非常奇怪的和违背牛顿运动定律的路径的这些数值通常相互抵消，总和很小，这就是量子波动的起源，即它们代表的路径总和很小。他更发现了通常意义的、牛顿学说的路径不相互抵消，因此总和最大，即它是具有最大概率的路径。因此，我们通常了解的宇宙只是无数个状态中概率最大的状态。但是所有可能的状态与我们共存，有些状态把我们带回到恐龙时代，有些把我们带到最近的超新星，有些把我们带到宇宙的边缘。而这些奇异的路径产生小的偏移，背离常识的、牛顿学说的路径，但是幸亏它们的概率很低。

    加来道雄教授进一步指出，费曼的“路径之和”的功能在于，今天当我们建立GUT（Grand Unification Theory，大统一理论）、膨胀理论，甚至弦理论时，我们都采用了费曼的“路径积分”观点。在全世界的每一个研究生院中现在教的就是这种方法，到目前为止它是最强大的、最便利的描述量子理论的方法。

    最后要说的是，我这两篇短文只能非常简单地介绍费曼——一个继爱因斯坦之后最睿智的理论物理学家的主要理论；而事实上，他的一生远比他发现物理理论更为精彩。他的一生告诉我们：我来过这个世界并且不虚此行。而我从他的一生中最受启迪的是，要一直采用犹如初生婴儿般的好奇心，看待与探索我们这个丰富多彩的世界。

    （作者系加拿大某国际财团风险管理资深顾问，科幻作家）