5月21日，嫦娥四号中继通信卫星 “鹊桥”成功升空。它的使命是前往地月拉格朗日L2点，为“嫦娥”和地球搭建一座用于通信联系的“桥梁”。那么，拉格朗日点到底是什么点？拉格朗日L2点又在天空的什么方向？

    三体问题中的五个特殊点

    拉格朗日点的提出者是被誉为18世纪欧洲最伟大数学家的拉格朗日。他的一生在数学、物理和天文领域都作出了重要贡献，其中之一就是系统性地提出了平面圆形限制性三体问题中的五个特殊解。

    三体问题研究的是三个可以被当作质点的物体，在给定任意初始条件时，在万有引力的驱使下的运动规律。科学家们花了几个世纪求解三体问题。然而直到今天，三体问题仍然无法精确求解，只在一些特殊情况下才可以得到答案。

    如果三体中一个物体的质量远远小于另外两个物体，它的引力对另外两个物体的轨道影响可以忽略不计，这种特殊情况就叫做限制性三体问题。拉格朗日研究的就是这种情况。他认为，如果两个质量较大的天体A和B以圆轨道互相绕转，求解一个相对质量可以忽略不计的第三个物体C的运动规律时，会存在五个特殊位置。把C放在这些位置上时，A、B、C三者的相对位置不变。这五个位置就是拉格朗日点。

    空间探测项目青睐的引力平衡点

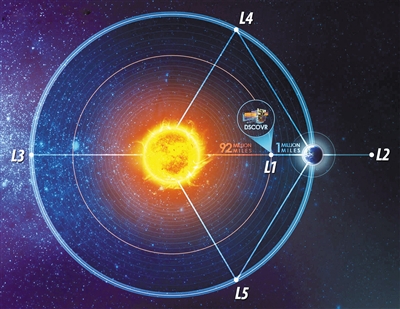
    我们可以在太阳和地球构成的系统中考虑拉格朗日点问题。假设地球围绕太阳作稳定的圆轨道运动，此时它受到太阳的引力和离心力平衡。这时，在日地中心连线上放一个小行星并忽略它对太阳和地球轨道的影响。在日地连线上存在这样一个位置，太阳和地球的共同作用恰好使得在这个位置上的小行星公转周期和地球一样长，于是三者始终保持在同一条直线上，也即三者的相对位置不变。这个位置便是L1点。

    如果把这个小行星放在日地连线的延长线上，也就是太阳和地球都在它的同一侧，那么在地球（较小质量的那个天体）背对太阳的方向上和太阳（较大质量的那个天体）背对地球方向上分别有两个位置点，处在那里的小行星公转周期和地球一样长，于是太阳、地球、小行星始终保持在同一条直线上。这两个点则分别是L2点和L3点。L2点的相对位置与三体中较大两个天体的质量比有关，质量差别越悬殊，该点相对越靠近较小质量的天体。

    日地系统的L2点被广泛使用。作为距离地球最近的两个拉格朗日点之一，L2点比L1点受到太阳光的危害更小更利于观测，因此在太空项目中使用率很高。例如，美国宇航局的威尔金森微波各向异性探测器和欧洲航天局的赫歇尔天文台都是利用了日地系统的L2点来观测。詹姆斯韦伯望远镜也会在不久的未来前往此处。

    此次“鹊桥”要前往的则是地月系统的L2点，也即月亮背对地球方向上的那个引力平衡点，距离月球中心约65000公里。在这里，“鹊桥”与月球同步公转，担任“嫦娥”与地球通信的信使。

    特洛伊小行星的聚集点

    除了日地连线上的三个点，在地球的公转平面上还有两个点，它们各自与太阳和地球构成一个等边三角形。换句话说，它们和地球共用一个圆轨道，只是一个超前地球60度（L4点），一个落后60度（L5点）。这两个点的美妙之处在于，当小行星处于这两个位置时，它受到太阳和地球的合力方向恰好指向日地系统的质心，合力大小又恰好满足公转所需的向心力。因此小行星在该处具有和地球相同的公转轨道。

    不仅如此，这两个位置的稳定性也很好，即使小行星在扰动下稍微偏离，也不会离去而是在围绕该点运动。基于这种稳定性，早在1772年拉格朗日便预言在太阳—木星系统的L4点或L5点可能会存在天体。1906年，德国天文学家马克思洛夫利用照相法发现了第一颗位于日木系统L4点处的小行星，从而证实了这个预言。

    随着同类型小行星的不断发现，人们将木星轨道上L4点和L5点的小行星统称为特洛伊小行星，并规定必须用特洛伊战争的人物命名这些位置上的小行星。于是第一个被发现的小行星被命名为希腊神话中的“第一勇士”阿喀琉斯（588 Achilles）。在科幻作品中，这两个特殊位置也常用于放置殖民卫星。

    （作者系香港大学地球科学系博士后）