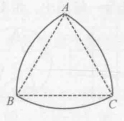
能否想象世界上有这样一种滚轮？它不是圆形却能使木板在轮子上平稳地滚动。能否想象有这样一种三角形？它有三个尖角，却有着许许多多圆的性质。这种不是圆形的滚轮，即三角形中的“叛徒”——鲁洛克斯三角形 （Reuleauxtriangle）。

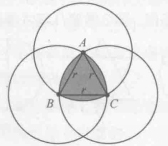
    鲁洛克斯三角形又称“勒洛三角形”“莱洛三角形”“圆弧三角形”。这种特殊的三角形是如何构造的？原来，它分别以正三角形的顶点为圆心，以其边长作圆弧，由这三段圆弧组成的曲边三角形。如果你曾经见过三个圆的维恩图，你现在或许就能找到一个隐藏着的鲁洛克斯三角形。对了！这就是维恩图正中间那个有三条弧边的三角形。

    那么，这样一个奇妙的三角形是怎么被发现的呢？这就要回到我们的滚轮问题上。如果把滚轮问题抽象成一个数学问题，那么地面和木板实际上就是两条平行线，而滚轮就是正正好好卡在平行线中间的图形，这就要求图形上每一个点到距离它最远的那个点的距离是一致的。鲁洛克斯三角形其实是一个等宽曲线。等宽曲线最初的定义是由一个十九世纪的德国工程师FranzReuleaux给出的：将一个曲线图放在两条平行线中间，使之与这两条平行线相切，无论这个曲线图如何运动，只要它还是在这两条平行线内，就始终与这两条平行线相切。这两条平行线间的距离称为等宽曲线的高度。鲁洛克斯三角形的特点是：在任何方向上都有相同的高度，即能在距离等于其圆弧半径 a（等于正三角形的边长）的两条平行线间自由转动，并且始终保持与两条直线都接触。

    除了做滚轮，鲁洛克斯三角形当然还有其他的作用，而且它往往在一些意想不到的地方发挥作用，比如鲁洛克斯三角形还可以做成打方孔的钻头。

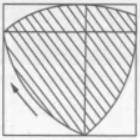
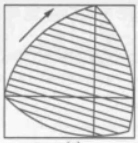
    由于鲁洛克斯三角形在一个边长为其宽度的正方形内转动时，任何时候都有四个点与正方形的四条边接触（不一定相切）且接触的位置是不断改变的，因而成了机械学家莱洛设计方孔钻头灵感的来源，而促使他发现了圆弧三角形和造出了方孔钻头。

    鲁洛克斯三角形这一特性，也被用于转子发动机，在这种发动机中，鲁洛克斯三角形的活塞就在正方形封闭体内旋转。马自达汽车发动机就是这样，当莱洛三角形转子转动的时候，转子边缘与转子壳体内壁之间会形成容积呈周期性平滑变化的 3个工作室，这三个工作室就相当于普通发动机中的三个气仓。普通发动机转一圈气仓体积变化一次，而转子发动机可以变化三次。这样转子发动机理论上就在同等转速的情况下拥有了三倍的马力。因为这样的性质，转子发动机汽车甚至被限制参加比赛。

    尽管鲁洛克斯三角形存在一些缺陷与不足，但是它还是很具有使用价值的。生活中那些我们司空见惯，习以为常的事情，能否找到第二种解法。看似功能一样的东西，如何利用它们的不同之处发挥其特质。这正是鲁洛克斯三角形的共同与不同带给我们的思考。

    （华中农业大学名师工作室数学文化团队成员）