任何一个数学描述，根据单位的不同，既可以是有理数，又可以是无理数。

    要用数描述任何东西，都离不开单位。比如，要描述两个苹果，用“个”做单位就是“2”（“2个”），用“对”做单位就是“1”（“1对”），用“半”做单位就是“4”（“4半”）。而且任何丈量单位都是人为的选择，中国人用尺，英国人用英尺，一般科学家用米，天文学家用光年，不存在哪一个比另一个更“理所当然”。

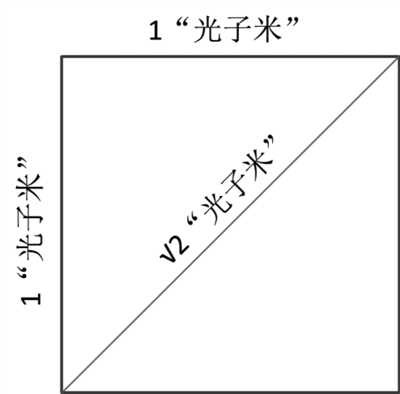
    要用数描述一个正方形的边长，也必须先选择长度单位。如果用边长本身作单位（权且叫它“光子米”），则边长为1“光子米”（如右上图所示），为有理数。

    假如选择边长为丈量单位

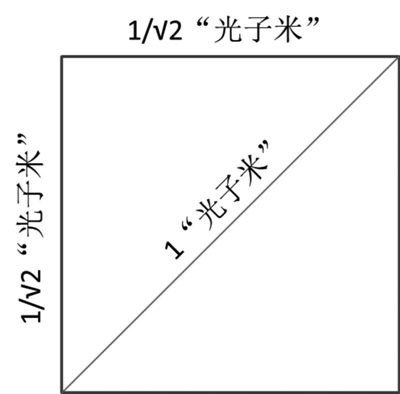
    但我们也可以选用对角线的长度做丈量单位。如果定义对角线为1“光子米”（如右下图所示），则边长为1/√2“光子米”i，是无理数。

    假如选择对角线为丈量单位

    同一条边长，因为丈量单位的不同，有时是有理数，有时是无理数！

    现实中的测量，如温度、速度等，都可以表示成一条线段的长度，所以它们都可以既是有理数，又是无理数。这说明任何描述都不是绝对的，会因为观察者所选取的单位的不同而不同。

    i根据勾股定理算出。1/√2=0.7071…，是无理数。