 |
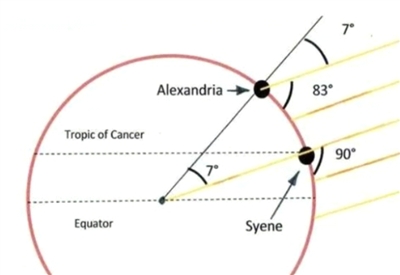
| 埃拉托色尼测量地球周长的原理 |
 |
| 古巴比伦的宇宙观 |
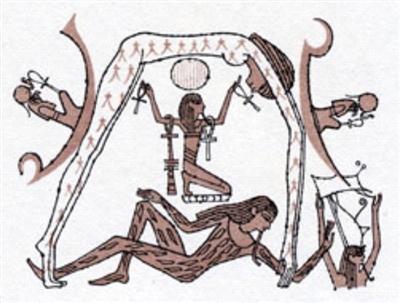 |
| 古埃及的宇宙观 |
 |
| 古印度的宇宙观 (本文图片源自网络) |
 |
《三国演义》中,刘备初次探访茅庐之时遇到了一位引吭高歌的农夫,歌中唱道:“苍天如圆盖,陆地似棋盘。世人黑白分,往来争荣辱。荣者自安安,辱者定碌碌,南阳有隐居,高眠卧不足”。歌词的深刻含义让刘备觉得非常人所做,遂有了茅庐三顾的故事。
笔者观看《三国演义》电视剧的时候,也对这段歌词印象深刻,不过当时只是觉得文辞优美,未作他想。不过后来却发现,其中有些有趣的问题。
地球上的几个重要的古文明都有自己的一套宇宙观,比如古巴比伦人觉得大地是被悬崖峭壁包围着的巨大海洋,人们生活的陆地在海洋中央,而天是纺锤形,像拱桥一样搭在包围大洋的悬崖峭壁上。古埃及人想象人们生活的大地是躺着的女神,上面的大气之神撑起了弯曲着身体的天神,太阳神和月神乘着小船每天横穿过尼罗河。古印度人觉得大地由三头大象支撑,大象下面踩着的是毗湿奴神变成的大乌龟,大乌龟又坐在化身为水的眼镜蛇上,眼镜蛇头尾相连的地方就是天。
“苍天如圆盖,陆地似棋盘”,则是我们中国人典型的宇宙观——“天圆地方”。自从“盘古开天辟地”以来,大地就像一片平整的方棋盘,而苍天就像一口大锅扣在上面。《敕勒歌》中“天似穹庐,笼盖四野”的句子也反映了这一观念。有趣的问题是: “如圆盖”的苍天是怎么扣在“似棋盘”的陆地上呢?“圆盖”如果外切于“棋盘”,有些部分的天下面就没有陆地;而如果“圆盖”内接于“棋盘”,则有一部分地没有天盖在上面。天地相接的边缘是什么样的呢?
不知诸位看官是否考虑过这个问题,或许您觉得这样的问题有点“理工科偏执狂”的倾向。其实在两千年前,屈原在《天问》就提出了这些问题:“九天之际,安放安属,隅隈多有,谁知其数”,九天的边际是如何安放在大地上的?圆形扣在地上,有多少弯弯曲曲的地方呢?
天圆和地方确实存在这个难以解决的问题,虽然古人也有个变通的办法,让天地不相接,用八根柱子把天从地面上撑起来(《天问》中“八柱何当”就指的是这八根柱子),形成像亭子一样的结构。粗略感觉这算是个解决方案,不过深究起来,却依然让人难以满意。因为我们身边还有一些现象和这个“方案”有所矛盾。
以下两首诗想必大家耳熟能详:
黄鹤楼送孟浩然之广陵
(唐 李白)
故人西辞黄鹤楼,烟花三月下扬州。
孤帆远影碧空尽,唯见长江天际流。
登鹳雀楼
(唐 王之涣)
白日依山尽,黄河入海流。
欲穷千里目,更上一层楼。
“欲穷千里目”为什么一定要“更上一层楼”呢?为什么“站得高”才能“看得远”呢?如果大地是平坦的棋盘,我们站在高处和低处看远方的景物,无非就是视角的区别,不应该看不见呀。如果你觉得地面上有很多障碍物,高处可以避开障碍物的话,那宽阔的湖面、江面、海面上没有什么障碍物了,为什么在“碧空尽”处总是“孤帆远影”而不是“孤船远影”呢?
从屈原的《天问》,到唐诗中对身边那些细节的观察,其实我们抓住过揭开大地之谜的线索。不过也许因为我们是个农耕文明,“孤帆远影”这样的场景在大家生活中太过细微,并未引起太多的在意。而航海发达的古希腊,可能由于在港口迎送远航的船只是很多人生活中不可缺少的部分,“孤帆远影”的现象广为人们关注,所以古希腊的先贤抓住这个线索探究了下去。
在距今大约2200年前,“地理学之父”埃拉托色尼用简单巧妙的实验测定了地球的周长。他在同一条子午线上找了两个地方:锡恩(Syene,今阿斯旺)和亚历山大港。锡恩附近的尼罗河一个河心岛洲上,有一口深井,夏至日那天太阳光在正午可以直射井底,而此时亚历山大港地面上竖的木杆阴影最短。用木杆和影子的长度之比,应用几何知识就可以知道太阳光射下的角度,与锡恩的太阳光角度之差是大约7°12′,是一个完整圆周360°的大约五十分之一,那么地球的周长就是这两地距离的50倍。按照今天的国际单位,埃拉托色尼测量的地球周长是39690公里,和现代科技测量的结果误差只有1%左右。
诗人和科学家有一个显著的共同点,就是敏锐的观察力。在读诗的时候,常常能看到那些平时被我们忽略的自然场景。在体味格律和意境的同时,不妨也试着思考,也许就能抓住一些自然留给我们的线索,去发现一些有趣的东西。
(作者系北京交通大学国家级物理实验教学示范中心教师,光学博士)







